|
铲齿和铲磨齿是滚刀加工中的两道主要工序,两道工序均在铲齿车床上进行。所用铲齿车床通常是丝杆导程为12.7mm的C8955等型号。文献[1]、[2]介绍了使用中如何计算滚刀的螺纹链挂轮,鉴于文献[1]在原理阐释上存在错误,而文献[2]又未给出实用方法,为此笔者提出一些具体方案供操作者参考。
1.挂轮计算的基本方法
首先求出所需的传动比i,并用近似分数值来表示,再将分子、分母分解成机床所具备的挂轮。此时常用公式如下:
i=nPx/12.7 1∶1 1
i=nPx/203.2 1∶16 2
式中 n——滚刀头数
Px——滚刀轴向齿距
实际计算时存在下列问题:
1为将i用分数表示,需进行因式分解等运算,计算者必须备有《挂轮选用表》等资料。
2有时计算所得挂轮机床并不具备,而更换一组挂轮又达不到精度要求。这样为求一副合适的挂轮,往往要耗费很长时间。
3求得的传动比i在表中查不到相应的分数值,而用邻近的分数值替代又达不到精度要求。
笔者在下面提出一些实用方法。
2.铲齿工序的螺纹链挂轮计算
该工序为滚刀加工的中间工序精加工工序,齿距公差较大,这使计算挂轮时有较大的灵活性。考虑到热处理对滚刀齿距的影响,铲齿工序要对成品齿距作一些修正,常用的经验公式为
P′x=0.998Px 3
式中 P′x——滚刀铲齿工序的轴向齿距
针对文献[1]、[2]的不足,提出三种实用计算方法。
1仅更换一只主动轮
由式1、3知:i=nPx/12.7,当n=1时,i=0.998Px/12.7=0.998mnπ/cosλ/12.7。一般单头滚刀λ≤5°,故cosλ≈0.998,即
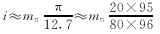
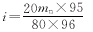 4 4
式中 mn——滚刀法向模数
λ——滚刀分圆柱螺纹升角
式4表示有三只挂轮是固定不变的,即95、80、96,按不同的模数,只要更换一只主动轮即可,其值为20乘以法向模数值一般齿轮滚刀标志及①单头齿轮滚刀;②铲床用1∶1的档位。
2一只被动轮为常数100,另一只被动轮可有针对性地选取
按P′i计算出i,再选定一被动轮b机床具备,得到b×i;取b×i的前四位数第五位按四舍五入处理作为一整数看待,将该整数分解成两主动轮的乘积。这样四个挂轮即全部确定,其中被动轮为人为选定的b及常数100。
如果两个主动轮之积在《整数因子表》中查不到,或分解后的挂轮机床不具备,则可更换原选定的被动轮b,然后按上述方法重新进行计算,直到满意为止。
例如在C8955铲齿车床上铲制某滚刀,其P′x=18.924mm,铲床用1∶16档位,则i=P′x/203.2=18.924/203.2=0.09312921;取b=144,则i×144=13.4070866,取前四位整数为1341,对其进行因式分解,而1341在因子表中查不到,故不能用。此时重新选取b=120,则i×120=11.17559055,取前四位数得1118,对其进行因式分解得1118=2×13×43=26×43。据此可写出挂轮如下: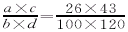 。经验算, 。经验算,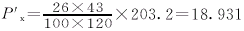 ,则ΔP′x=0.007。在一般情况下,当铲齿工序挂轮误差ΔP′x在0.01mm左右即可满足使用要求,现ΔPx′=0.007mm,故此挂轮完全适用。 ,则ΔP′x=0.007。在一般情况下,当铲齿工序挂轮误差ΔP′x在0.01mm左右即可满足使用要求,现ΔPx′=0.007mm,故此挂轮完全适用。
3预先确定法
所用四只挂轮中,有三只系人为预先确定,从预先确定的挂轮可计算出第四只挂轮,并可及时判定第四只挂轮是否适用。此方法不需使用《挂轮比表》、《整数因子表》等资料,但需一只能够贮存公式的袖珍计算器,操作简单,限于篇幅,拟另文介绍。
3.铲磨齿工序的螺纹链挂轮计算
该工序为滚刀的精加工工序,加工出的齿距精度即为成品精度,必须符合相应标准的规定,一般均以μm计算。前述铲齿工序所用方法难以达到这种高精度要求,因此,应考虑其它计算方法。
铲磨齿工序传动比i按1式或2式计算。但应注意,由于各台机床性能的差异有时因操作者不同而出现性能差异,虽然理论上要以Px来计算挂轮,但实际上往往要对Px作微量修正,增加或减小若干μm,修正后的Px值称为特定需要值。例如某机床加工m4滚刀,Px=12.583,按此计算所用挂轮铲磨出的滚刀齿距却不合格,需增大2μm,即按12.585计算方能合格,12.585即为特定需要值,大于或小于此数值均不行,只能按12.585来计算,不能按理论值或其它值计算。
由于该工序精度要求高,往往会遇到前述“基本方法”中所指出的问题。例如某滚刀特定需要值Px=17.778mm,用1∶16档次求挂轮,要求挂轮所得误差ΔPx<1μm。按式2得传动比i=Px/203.2=17.778/203.2=0.08749。查《挂轮比表》无此数值,只能用邻近数值替代,即0.08748=58/663,经验算Px=17.776,ΔΡx=-2μm;另一替代表值0.08750=7/80,经验算Px=17.780,ΔPx=+2μm,两个结果均不符合要求。此时,可用下述方法解决:
1求传动比i;
2人为选定一被动轮d,得i′=d×i;
3按i′小数点后的尾数查表得出相对应的分数值为A/b查表时,不必严格对应,可在邻近几行乃至十几行查对,这是本方法的较大优点和特点,查对时选用的分母b应是机床具备的挂轮数;
4由上序得i′=整数部分+A/b,通分后为i′=F/b;
5查《整数因子表》得出F=a×c;
6写出挂轮: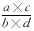 a×c为第5步确定值,b为第3步确定值,d为第2步确定值。 a×c为第5步确定值,b为第3步确定值,d为第2步确定值。
7校对精度。
计算过程中应注意以下问题:①有时按第5步查表时无相应数值,此时应重新返回第3步,另取一组A/b值后再次查表。②如精度仍不能满足要求,或有其它不便时,可返回第2步,另选d值后再进行运算。
上例按本文提出的方法计算,可得:
1i=Px/203.2=17.778/203.2=0.08749;
2取d=135,i′=135×i=11.81117;
3在《挂轮比表》中查i′的尾数0.81117相对应的分数值为494/609,因分母609不是机床具备的挂轮数,故不用。于是在邻近表中查找分母是机床具备的挂轮b的简单数,找到0.81102→103/127,故取A/b=103/127;
4于是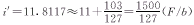
5查表得1500=2×2×3×5×5×5=30×50a×c;
6写出挂轮: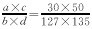
7验算: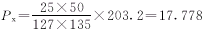 ,ΔPx→0,符合要求。 ,ΔPx→0,符合要求。
4.小结
挂轮计算的通用原则是采用“基本方法”,在铲床上加工滚刀时螺纹链的计算则视工序不同而有多种方法。粗加工工序较灵活,运用4式即可满足绝大部分单头齿轮滚刀的计算需要,通常ΔΡx为0.01mm左右即可。精加工工序则应计算精确,运用本文所述方法可保证算出任何一组PxΔPx<1μm的挂轮,且查表时数值选择范围较大;其中被动轮是人为确定的,计算简单方便,无需复杂的推导过程。
编辑
|
