摘要 提出了一种在参数坐标系下自适应步长和行距的计算方法,该算法考虑了不同刀具接触点处的曲率差异,在满足加工精度和粗糙度的前提下,又能有效地提高加 工效率。该算法适合加工汽车车身模具等曲率变化大的曲面。文中还给出了刀位计算公式。
关键词 平头立铣刀 自由曲面 五轴数控加工 刀具轨迹
An algorithm for calculating 5-axis cutter path on sculptured surfaces with flat-end milling cutter
Li Xiaoping Yu Daoyuan Tang Yangping Duan Zhengcheng
Abstract:This paper presents a new algorithm of adaptive step lengt hs and path interval on parametric coordinate system.As the algorithm considers the radius of the curvature difference between different cutter contact points, so it can improve machining efficiency and the accuracy of the finished surface. This algorithm is suitable for machining sculptured surface. A method of calcul ating cutter location point is also presented in this paper.
Key Words:flat-end milling cutter,seulptured surface,5-axis NC machining,cutter path
1 前言
自由曲面在模具中应用非常广泛,如汽车车身模具、塑料模、叶片锻模、铸模等,大都包含自由曲面以下简称曲面。曲面的加工通常由球面刀和非球面刀如平头立铣刀、锥状刀、鼓形刀等完成,由于平头立铣刀以下简称立铣刀的切削效率、加工质量、使用寿命等都优于球面刀[1],应优先选择。近几年来,国内外有关曲面立铣刀五轴数控加工轨迹的算法的研究较多[4~6],这些算法用微分几何的方法对步长和行距进行预测,公式简单,计算量小,但它们没有考虑相邻刀具接触点间曲率的变化,对于加工曲率变化小的曲面比较有效,不适合曲率变化大的曲面。本文提出一种在参数坐标系下自适应步长和行距的计算方法。该算法在满足加工精度和粗糙度的前提下,又能有效地提高加工效率,适合曲率变化大的曲面的加工。
2 刀具的有效半径
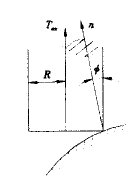
五轴立铣加工曲面时,由于立铣刀的切削刃在立铣刀的周边上,所以立铣刀的轴线与曲面的法线之间应当偏置一个刀具半径,方能有效地切削曲面。考虑到刀具与曲面干涉等因素,立铣刀在偏置的同时,其轴线在被加工点的法平面内还应与法线夹一角度φRe=Rsinφ。在
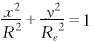 (1) (1)
 d=r(wi,u)-r(wi,0)-λc (2)
d=r(wi,u)-r(wi,0)-λc (2)
式中:λ——系数,λ∈[0,1]。
由于c与d垂直,可得到:
cd=0 (3)
联立式2、(3)解得:
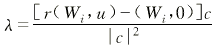 (4) (4)
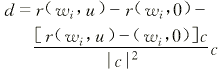 (5) (5)
上式可以写成:
d=P[r(wi,u)-r(wi,0)] (6)
其中,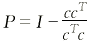 ,称为投影矩阵,I为单位矩阵。 ,称为投影矩阵,I为单位矩阵。
由于在弦向偏差较大处,曲线切矢垂直于矢量d,即r′((wi,u)d=0 (7)
故r′((wi,u)P[r(wi,u)-r(wi,0)]=0 (8)
上式中除两端点为根外,还有多个根,由于在弦向偏差较大处,存在:
r″(wi,u)d<0 (9)
所以把式(8)和u∈0,1用于每一个根处,式(7)中满足式(8)和u∈0,1的根即为较大偏差处相应的u值,因此,可求出δt。
上述算法过程中,首先必须检查曲线段内有无拐点,并计算出该点的位置。若曲线段有拐点,则以此拐点将曲线一分为二,将两段参数曲线的区间[u1,u2]转换到[0,1]区间,分别对两段曲线采用二分法进行迭代。
3.2 刀轴摆动误差的计算
刀轴摆动误差是加工过程中,由于刀具轴向矢量摆动引起的非线性误差(见
|δn|≤Re(kf.ΔSu) (10)
式中:kf——直线逼近段内曲面沿进给方向在较大直线逼近误差点处的法曲率;
ΔSu——逼近段弧长。
ΔSu=∫u2u1|r′Wi,u|du (11)
当kf<0时,加工表面沿走刀方向为凸曲线,刀具接触点的轨迹为凹曲线,因此,加工误差为直线逼近误差和刀轴摆动误差绝对值之和,即:δ=|δn|+|δt|。
当kf<0时,加工表面沿走刀方向为凹曲线,刀具接触点的轨迹亦为凹曲线,且刀轴摆动误差|δn|总是小于直线逼近误差|δt|,因此,可视直线逼近误差|δt|为加工误差δ,即:δ=|δt|。
4 自适应行距的计算
虽然曲面的形状各异,但是刀具在加工这些曲面时,都是按照一定的曲线走刀加工出整张曲面的。对于刀具接触点而言,根据其所在曲线在该点处的曲率大小可以分为三类:凸点、凹点、拐点,在这里将直线上的点也归为拐点类。凸点、凹点、拐点可以根据其曲率kf的大小加以判别:
当kf>0时,为凸点;
当kf<0时,为凹点;
当kf=0时,为拐点。
与凸点、凹点、拐点相对应,这些点所在的曲线可以分为凸曲线、凹曲线、直线。当刀具的接触点是凸点、凹点或拐点时,在密切面内,这三类点邻域的曲线可以分别看成是凸圆弧、凹圆弧和直线。因此,在计算自由曲面的行距时,可以直接在圆弧和直线上加以计算。
x=(ρ+h)sinα
y=(ρ+h)cosα-(ρ+Rsin)
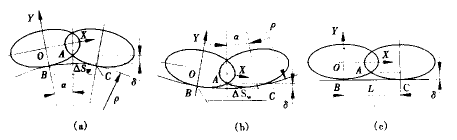
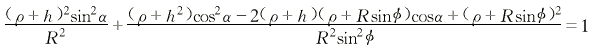
这是一个一元二次方程,可解出h:
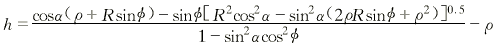 (12) (12)
对于
Tc1=n-Tax1=n-|ncosφ|Tax
又cosφ=nTax,故:
Tc1=n-(nTax)Tax
单位化矢量Tc:
Tc=Tc1/|Tc1| (17
其中刀具轴矢量Tax可将单位法矢量n在A点法平面内旋转φ角得到,即:
Tax=nTR (18)
上式中TR为旋转变换矩阵:
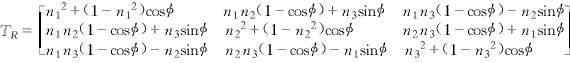
式中:n1、n2、n3——旋转轴单位矢量的方向余弦。
于是,刀具中心点的轨迹为:
Ce=r(w,u)+RTc (19)
6 结论
本文采用弦差法计算五轴立铣刀加工曲面的直线逼近误差,依据微分几何关系计算在较大直线逼近误差处刀轴摆动误差,由两者构成的加工误差来共同控制加工步长,该算法考虑了不同刀具接触点处的曲率差异。文中还对行距计算公式进行了推导,给出了刀位计算公式。该算法适合加工曲率变化大的曲面。
|
