快速成型切片数据

摘　要：为了能够顺利地进行STL模型切片轮廓数据的进一步处理，提出了对切片数据进行优化处理的算法。对由于STL模型的缺陷造成切片之后的轮廓信息数据有大量的冗余数据，提出了一种冗余数据的滤除算法；针对切片轮廓的不封闭，给出了有效的修正算法；同时给出了对切片轮廓的内外边界进行自动识别的算法。该算法高效简单，提高了后续的数据处理的效率和成型件的加工质量，改善了零件成型的加工性能。
关键词：快速成型制造；STL文件；数据优化

1　引　言

快速成型技术(RapidPrototypingTechnology)是一种基于离散堆积成型思想的新型成形技术[1]，自80年代产生以来得到了迅速的发展。由于其具有生产的敏捷性、制造技术的高度集成化以及适合于制造几乎任何形状等的优点广泛应用于机械、电子、汽车、玩具、通讯、航空航天等领域。其基本制造原理为：将CAD模型在计算机内用切片软件沿Z方向切片离散，得到一系列具有一定厚度的薄片，然后激光束(或紫外光束)在计算机的控制下在二维的切片层面上固化或粘结某一区域，从而形成零件实体的一个层面，随后再同样固化下一个层面，如此反复，逐渐堆积便形成一个三维零件。快速成形技术根据制造工艺的不同可以分为：叠层实体制造(LOM)、选择形激光烧结(SLS)、光固化法(SL)、熔融沉积制造法(FDM)、三维立体印刷法(TDP)等。

STL文件是CAD实体数据模型经三角化网格化处理后的数据文件，是用许多空间三角形小平面逼近原CAD实体模型，因为STL文件格式简单而且不需要复杂的CAD系统支持，现在已经发展成为CAD系统与快速成型系统之间数据交换格式的不成文标准。尽管STL文件在快速成型领域有着极其广泛的应用，但是其缺点也是十分明显的，例如缺少三角面片之间的拓扑信息，而且还会有裂缝、间隙、面片重叠和法向量反转的错误[2]。由于STL文件所固有的缺陷，使得切片之后得到的轮廓信息有大量的冗余数据，甚至会产生轮廓线不封闭等错误。如果我们不对这些冗余数据和错误不加以处理，就很难进行以后光斑的半径补偿等以后数据处理，影响零件加工的稳定性和加工效率，甚至不能成型正确的零件形状。因此对截面轮廓数据进行优化处理就显得十分的必要。

2　切片轮廓数据的特性

STL文件用许多空间小三角形来表示零件的表面，对每一个空间小三角形面片用三角形的三个顶点的坐标及三角形面片的法向量来描述，法向量由零件的内部指向外部，三角形三个顶点的次序与法向量满足右手规则。

STL文件中每相邻的两个三角形只能有一条公共边。STL文件有两种格式，一种是ASCII格式，另一种是二进制格式。ASCII格式的STL文件具有可读性，但占用较大的空间，大约是二进制STL文件的五倍。

ASCII格式的STL文件结构如下：

solid ASCII　　　　　　　　　　　//ASCII为文件名
facet normal nx ny nz//三角形面片的法向量
　　outer loop
　　　　vertex V1xV1yV1z//顶点V1的坐标
　　　　vertex V2xV2yV2z//顶点V2的坐标
　　　　vertex V3xV3yV3z//顶点V3的坐标
　　end loop
end facet

在快速成型技术中，对模型的切片过程实际上就是一个平面和平面求交的过程，也就是由平行于XOY的一系列平行平面和组成模型的三角面片求交的过程。实际上这个过程也可以认为是直线和平面的求交，即组成三角形面片的三条边和平行于XOY平面的求交。在这个过程中，首先选取切片平面(z=zi)，然后在STL文件中搜索与这个Z平面相交的所有三角面片，记录下这样的一个个交点，假如STL文件没有错误的话，就会得到一系列Z值不相同的封闭的截面轮廓多边形。

STL切片之后的截面轮廓信息是指由一系列有序点集，顺序连接构成的多个折线。其中第i条折线的点集为：

Vi={v1，v2，…，vn}其中n为点数。

它们必须符合三条规则：

1这条折线应该是简单的封闭的，构成一个多边形。不应该存在自相交和不封闭的情况，自相交的情况很少出现，本文只对比较常见的轮廓不封闭给出了相应的算法。

2vn是足以描述这条折线的最少的点。其中不应该存在多余的数据点，本文对于冗余点的去除提出了一种有效的算法。

3切片之后得到多条封闭的折线形成的截面多边形组成实体区域的边界，必须对这些边界识别并进行方向性处理，其正向规定为：沿封闭折线前进时，区域总保持在左侧，如

struct Head
{
floatLayHeight；　　//该层轮廓的高度
boolInOrOut；//内外环标志，外环为0
boolHaveBug；//错误标志，轮廓有错为1
DataPoint*Pointer；//指针　
}

数据节点为：

struct DataPoint
{
floatXdata，Ydata；//数据点的x，y坐标
boolHaveGap；//断点标志
DataPoint*Pointer；//指针
}

在本文中，如果轮廓不封闭，在头节点置错误标志；在断开处，置数据节点的断点标志。如

(1)调入轮廓信息的链表，检查头节点的错误标志，如果该链表没有错，调入新的链表；如果链表有错，进入(2)。
(2)搜索链表各个节点的断点标志，找出所有断开点。
(3)计算各个断开点之间的距离，连接距离较近的断开点，并且修正各段轮廓线的方向。如

实际上是计算三角形APB的面积，如果下式：

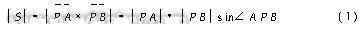
|S|≤ Q，( Q为定义的误差范围)。(2)

成立，则可以去掉点A。