关键字:

	胡锦涛在辽宁考察称我国

首页 >> 机床技术资讯 >> 查看资讯信息

圆管剪切原理和切刀圆角半径的确定

来源：信息中心　时间：2009-2-1 10:21:03

管切断采用冲裁方法已很普遍了。关于圆管剪切的受力分析、切刃的几何形状、切刀圆弧半径的确定或弧半径与管半径之间联系等问题的解决，对于圆管切断模刀刃设计具有重要意义

一、圆管切断外推力的条件

为了保证管材在剪切过程不发生向内塌陷，必须使切刃对管壁始终产生一个由内向外的推力。

θ＜90°-β-α(1)

式中θ——方管上管壁与y轴夹角
α——摩擦角

由于是方管β＝45°，则

0＜θ＜45°-α(2)

在第4象限时(

(-90°-(α`－β`＜θ`＜90°-(α`－β`)(3)

式中θ——切刃与y轴夹角
β——方管下管壁与y轴夹角
α＝α为摩擦角

由于是方管β`＝β＝45°，故有

0＜θ`＜135°-α(4)

0＜θ≤45°-α

管剪切时，产生外推力的条件，根据以上的推理可知只要满足式(1)即可，不过式中的θ与β角都必须变化，且θ定义为刀具形状切线与y轴夹角，β为管壁切线与y轴夹角，α仍为摩擦角，α＝arctanμ。μ为钢对钢的动摩擦系数，在有润滑时为0.05～0.1，在无润滑时为0.15；钢对软钢在有润滑时为0.1～0.2，在无润滑时为0.2。为了安全，一般取μ＝0.2，则α＝11°19≈12°，则可得圆管剪切外推力几何条件为

0≤θ≤90°-12°-β

即0≤θ≤78°-β (6)

由

AB＝Rsinγ
OB＝Rcosγ

式中R—圆管半径

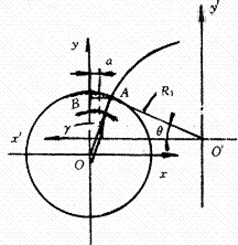
x1＝R1cosθ
y1＝R1sinθ

由图中几何关系可得

Rsinγ＝α+R1(1-cosθ)

则

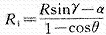
式中R1——切刃圆弧半径

α＝Rsinγ0＝Rsinα(11)

由(10)式可知，剪切刀片切刃圆弧半径是变化的，不是定值，即刀刃的形状曲线不是圆形。不过为解决此问题，可采用另一途径，即取某一半径R1值代入(10)式，可以求出γ的角度值，然后验算看是否能满足(9)式，如能满足，则可行，如不行，说明必须另求其它曲线。不过其它曲线不能满足(7)、(8)式。

以剪切R＝10mm的圆管为例进行计算。首先以R＝10mm和α＝12°代入(11)式，求得a＝2.97mm。其次以R＝10mm，a＝2.1mm，R1＝135.9mm代入sinγ＝［R1(1-cosθ+a］／R，除在θ＝5°～8°的范围内求得γ值不能满足(9)式外，在其它θ值下求得的值均能很好满足(9)式。根据以上分析，切断刀片可以选用一大圆孤半径作为刀刃的半径。图6画出了几种不同圆角半径刀片的形状。

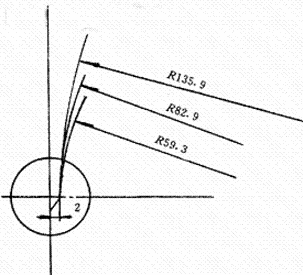图6

从切断面质量要求来看，圆弧半径R1要大；从强度要求来看，圆角半径R1要小。对于剪切R＝10mm的圆管来说，选用R1＜59.32mm为宜。

三、结论

(1)通过分析，导出圆管剪切时产生外推力的几何条件。
(2)为确定剪切刀片刀刃圆弧半径R1提供了一种思路。

【关闭窗口】【打印该页】

本信息真实性未经证实，仅供您参考。未经许可，不得转载。