|
|
刀具半径补偿干涉检验的向量算法 |
| 来源：信息中心 时间：2009-2-1 10:25:52 |
|
|
1 干涉的产生
由于被加工零件轮廓的不确定性和复杂性，当刀具的半径过大或者遇到轮廓的内尖角时，如果处理不好刀具在轮廓过渡处的轨迹，就会出现刀具过切轮廓的现象(缩短型、伸长型和插入型。
相邻两段轮廓的切线在交点处工件侧的夹角，称为两段轮廓的夹角((1)左刀补：s>0时，为缩短型;s≤0时，为非缩短型;(2)右刀补：s<0时，为缩短型;s≥0时，为非缩短型。
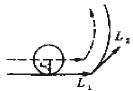
- 对于直线AO由l1与l2方向相反，即
| l1+ l2= 0 |
(4) |
- 对于圆弧OB 设圆心C相对于起点O的坐标为I、J，终点B相对于起点O的坐标为Xe、Ye。设圆弧起点O到圆心C的向量为OC，圆弧终点B到圆心C的向量为BC，则
OC= Ii+ Jj
BC= (I- Xe)i+ (J- Ye)j
- 设交点O1到点C的向量为O1C，圆弧终点B补偿后的点B1到点C的向量为B1C，B点的刀具半径向量为TB=Xtbi+Ytbj，则
O1C= (I- XO1)i+ (J- YO1)j
B1C= (I- Xe- Xtb)i+ (J- Ye- Ytb) j
- 圆弧干涉的条件是向量OC和BC的叉积在它们所在平面法线K上的投影与向量O1C和B1C的叉积在K上的投影方向相反，即
| [(OC× BC)·K][(O1C× B1C)·K]<0 |
(5) |
- 以上分析的是直线接圆弧的情况，对直线接直线和圆弧接圆弧的情况可以进行类似的分析：对于直线，按式(4)，若补偿前后的向量方向相反，则产生干涉，否则不产生干涉Z对于圆弧，按式(5)，若补偿前后的圆弧方向相同，则不产生干涉，否则干涉。
4 结束语
- 本文提出的干涉检验算法已经在本所开发的数控系统中采用，经过长时间的应用和生产检验，被证实是切实可行的、是快速有效的。它能够检验两段轮廓干涉的全部情况，满足干涉检验的基本要求。
| 【关闭窗口】【打印该页】 |
本信息真实性未经证实，仅供您参考。未经许可，不得转载。 |
|
|
| |
首页 >> 机床技术资讯 >> 查看资讯信息 
